當需要測量的物理量為矢量時，我們需要使用三個正交放置的傳感器來分別測量物理量的各個分量，以此來合成一個完整的矢量。如果我們對測量精度要求非常高，就不能僅僅只是對單個傳感器進行修正，還要考慮三個傳感器的敏感軸是否嚴格的正交。很多時候我們需要仔細的調整三個傳感器的正交關系，但是將三個傳感器調整到完全正交是很難的，并且許多時候，由于設計等原因，這種機械上的調校是無法進行的。這時，軟件修正就成了必不可少的步驟，軟件修正大多數時候也比機械上的調校更簡單。

 

這里介紹一種基本的軟件修正方法。它對大多數類型的傳感器都可以使用。首先，假設單獨的每個傳感器的測量的值都是準確的，這可以通過預先對每個傳感器進行標定來完成。

 

這里設三個傳感器的測量值分別是 x1，x2，x3。這三個值可以合成一個列向量X：

所謂軟件修正算法，就是找到從 X到 Y 的映射。由解析幾何知識我們知道X到 Y 的映射可以通過一個線性變換C來表示：

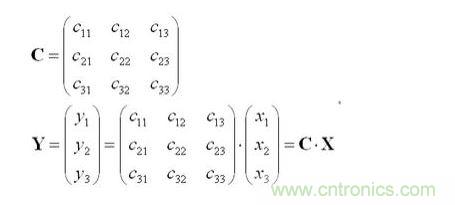
寫到這里其實方法就很明了了，我們只需要求得這個轉換矩陣C就一切都解決了。

 

轉換矩陣C如何求，當然是通過大量的測量數據來擬合。實驗數據的獲得很重要，最好能有個比較精密的三軸轉臺，這樣轉各個角度都比較方便。沒有也沒關系，但至少要能把裝配好的傳感器組沿三個已知的方向放置，并且這三個方向要擺放的很精確。通常，我們選的這三個方向是相互正交的，這三個方向上物理量的真實值就是上面式子中的y1、y2、y3，換句話說這三個方向是三個傳感器的名義上的取向，雖然這三個傳感器可能全都擺歪了。具體如何采集數據就不詳細描述了，由于未知參數有9個，至少要采集9組數據才行，條件允許的話當然是數據越多越好。

下面說說如何對采集到的數據進行擬合。通常我們遇到的最小二乘擬合問題的待擬合的函數都可以表示為：

這個問題已經有成熟的算法，各種常見的數學軟件，比如 Matlab、Mathematica、scilab、Lingo 等都有現成的程序包來完成這個計算。我們現在的問題難點在于 y 也是個向量，這就需要我們對上面的方法進行一點簡單的變形。簡單的說，我們實際上是有三個待擬合函數的，因此g(C)也要做相應的改變：

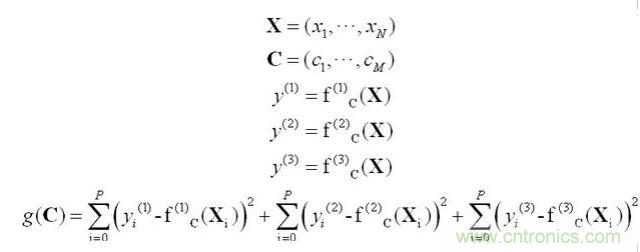
經過這樣轉化后就成了一個普通的最優化問題（函數求極值）了，各種數學軟件都可以方便的計算出結果。

 

這里再多說幾句，我個人喜歡使用 gnuplot，gnuplot中有個 fit 命令，也可以完成多元函數擬合。Gnuplot的 fit 命令采用非線性最小二乘 (NLLS) Marquardt-Levenberg算法，擬合能力非常強悍，只要擬合參數的初值給的別太離譜，基本都能夠收斂到最優解上。fit命令具體的用法可以參考gnuplot的幫助文件。這里只講講如何處理 y是多個值的問題，方法很簡單，就是通過多引入一個自變量，將多值函數改造成普通的函數：

這里需要注意的是如果a1，a2，a3成為未知數，c11，c22，c33就可以作為已知量了，比如設c11=c22=c33=1，因為這里的六個未知數只有三個是獨立的。因此，實際上只增加了三個未知數。

 

如果將上面的方法和溫度修正一起考慮的話可以這樣處理：

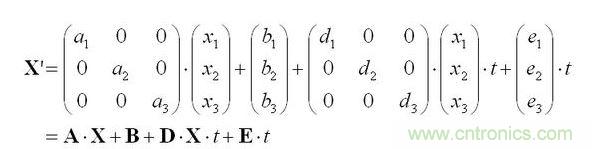
上面式子中的t是溫度，這里的溫度修正算法比較簡單，主要是為了盡量少引入未知的參數。后面的計算就沒什么不同的了。